Spis treści:
1. Linie długie, transformacja impedancji przez linię długą
2. Transformatory z linii długiej (transmission line transformers – TLT), transformator symetryczny 1:9

W poprzedniej części zajęliśmy się liniami długimi i ich właściwościami. W tym wpisie wykorzystamy te linie do budowy ciekawszego urządzenia, jakim będzie transformator impedancji.

W technice w. cz., szczególnie większej mocy, często można spotkać się z transformatorami wykonanymi z linii długiej (transmisyjnej), najczęściej z przewodu koncentrycznego. Transformatory takie wykorzystują bardzo dobre sprzężenie między przewodnikami w linii długiej, tym samym pozwalając na stworzenie szerokopasmowych i (stosunkowo) niskostratnych transformatorów. W transformatorach tego typu nie ma separacji galwanicznej między obwodami. Po angielsku zwane są transmission line transformers, w skrócie TLT.

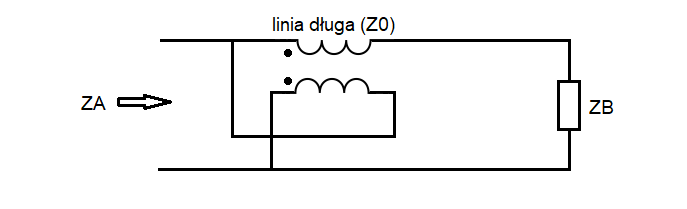
Na rysunku 1 przedstawiono niesymetryczny transformator o przełożeniu impedancji 1:4 wg opisu Ruthroffa. Przez dwie cewki oznaczono linię długą o impedancji falowej $Z_0$. $Z_A=\frac{Z_B}{4}$ dla (lekko abstrakcyjnego przypadku – ale udowadnialnego matematycznie) linii długiej o zerowej długości. Dla niezerowej długości linii przełożenie impedancji zaczyna być zależne od impedancji falowej linii i jej długości.

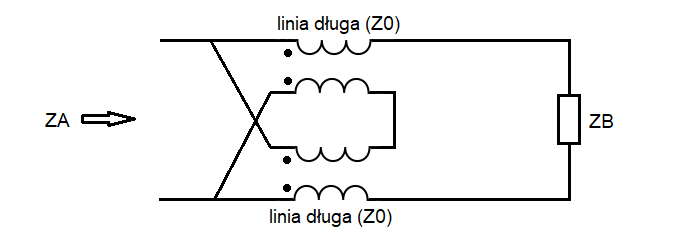
Na rysunku 2 przedstawiono symetryczny transformator o przełożeniu impedancji 1:4 wg opisu Guanelli. Obydwie linie długie mają identyczne długości i impedancje falowe. Podobnie jak poprzednio, dla abstrakcyjnego przypadku linii o zerowej długości, przełożenie impedancji jest równe $Z_A=\frac{Z_B}{4}$. Dla linii o niezerowej długości będzie zależne od długości linii i jej impedancji falowej. Tego typu transformator jest często używany jako transformator wyjściowy we wzmacniaczach mocy, gdzie elementy aktywne działają w układzie przeciwsobnym (push-pull).

Osoby, które pierwszy raz spotykają się z tego typu transformatorami mogą się mocno zastanawiać, jak to w ogóle działa. Niestety analiza takiego obwodu w oparciu o model typowego transformatora raczej nie doprowadzi nas do żadnych wniosków, a już na pewno nie pozwoli uwzględnić właściwości linii długich, które mają tutaj kluczowe znaczenie.
W takich transformatorach trzeba wziąć pod uwagę wzory opisujące linie długie i w taki sposób przeanalizować obwód. Linie długie i wzory, których będziemy potrzebować, zostały omówione w pierwszej części tej serii.
Pokazane wyżej transformatory to tylko dwa z wielu, które można wykonać. Zostały one przytoczone jako przykład m. in. dlatego, że już omówił je kolega K6JCA na swoim blogu i bardzo polecam zapoznać się z tym opracowaniem. Niemniej po dzisiejszym wpisie czytelnik powinien poradzić sobie z analizą powyższych układów samodzielnie, gdyż zajmiemy się innym, trochę bardziej skomplikowanym transformatorem.

W tym wpisie przeanalizujemy transformator symetryczny o przełożeniu impedancji 1:9, który bardzo często pojawia się w schematach wzmacniaczy mocy na tranzystorach LDMOS na pasma KF. Powodem tej analizy jest to, że nigdzie nie udało znaleźć mi się obliczeń dla takiego transformatora. Układ wygląda jak przedstawiono na poniższym rysunku.

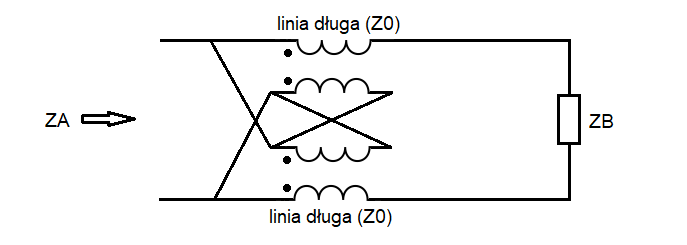
Nie udało mi się ustalić, skąd tak naprawdę pochodzi ten układ. Można jednak zauważyć, że od transformatora 1:4 Guanelli różni się tylko połączeniem prawych stron wewnętrznych indukcyjności na „przeplot”, a nie bezpośrednio do siebie (jak w przypadku 1:4). To przeplatane połączenie powoduje, że układ ten jest bardziej skomplikowany w analizie. Zaznaczmy zatem napięcia i prądy w tym obwodzie.

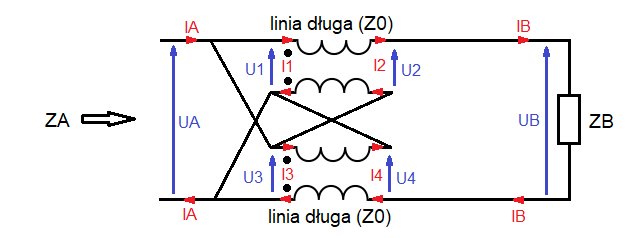
Przyjmujemy, że linie mają długości $L$. Pojawiło się dość dużo tych oznaczeń, więc na początku sprawdzimy, co można uprościć. Od razu widać, że $U_A=U_1=U_3$ (połączenie równoległe), a także że $I_2=I_4=I_B$ (połączenie szeregowe). Dalej analizując prądy dochodzimy do wniosku, że $I_A=I_1+I_2+I_3$. Po dokładniejszym przyjrzeniu się można zauważyć też, że $U_B=U_1+U_2+U_4$. Nadal zostaje sporo zmiennych. Układ jest symetryczny, więc nasuwa się pytanie, czy $U_2=U_4$ oraz czy $I_1=I_3$?
Przypomnijmy rozwiązania równań linii długiej (oczywiście stosuję już uproszczenia, które ustaliliśmy przed chwilą):
\begin{align*}
U_4=U_{1}\cos{\beta L}-jI_{3}Z_{0}\sin{\beta L} \\
I_3=I_{2}\cos{\beta L}+j\frac{U_{4}}{Z_{0}}\sin{\beta L}
\end{align*}
oraz
\begin{align*}
U_2=U_{1}\cos{\beta L}-jI_{1}Z_{0}\sin{\beta L} \\
I_1=I_{2}\cos{\beta L}+j\frac{U_{2}}{Z_{0}}\sin{\beta L}
\end{align*}
W pierwszym układzie równań podstawiamy za $I_3$, a w drugim za $I_1$, wymnażamy i otrzymujemy:
\begin{align*}
U_4=U_{1}\cos{\beta L}-jI_{2}Z_{0}\sin{\beta L}\cos{\beta L}+U_{4}\sin{^2\beta L} \\
U_2=U_{1}\cos{\beta L}-jI_{2}Z_{0}\sin{\beta L}\cos{\beta L}+U_{2}\sin{^2\beta L}
\end{align*}
Po przeniesieniu na jedną stronę wyrazów z, odpowiednio, $U_2$ i $U_4$ i porównaniu równań stronami otrzymujemy:
\[ U_4(1-\sin{^2\beta L})=U_2(1-\sin{^2\beta L}) \]
Teraz przyjmujemy założenie, że $\sin{^2\beta L}\neq 1$, co jest równoznaczne z tym, że linia długa ma długość różną od ćwierci długości fali lub jej nieparzystej wielokrotności (bo wówczas sinus przyjmuje wartość 1 lub -1). Wtedy możemy bezpiecznie podzielić obustronnie i otrzymujemy:
\[ U_4=U_2 \]
Jak widać napięcia te są sobie równe pod warunkiem, że linia długa ma długość $L\neq (2n+1)\frac{\lambda}{4}, n\in N_0$. W innym przypadku napięcia te nie muszą być sobie równe.
Analogiczne rozumowanie przeprowadzamy dla $I_1$ oraz $I_3$, tym razem po prostu podstawiając w układzie równań za $U_2$ i $U_4$. Ostatecznie dochodzimy do podobnego wniosku:
\[ I_3=I_1 \]
o ile $L\neq (2n+1)\frac{\lambda}{4}, n\in N_0$.

Możemy teraz przystąpić do właściwych obliczeń.
Linia o długości różnej od długości ćwierci fali lub jej nieparzystej wielokrotności

Linia ma długość różną od długości ćwierci fali lub jej nieparzystej wielokrotności, więc $\sin{\beta L}\neq 1$, zatem spełniony jest warunek na równość napięć $U_2=U_4$ i prądów $I_1=I_3$.
Z prawa Ohma wiadomo, że:
\begin{align*}
Z_A=\frac{U_A}{I_A}=\frac{U_1}{2I_1+I_2} \\
Z_B=\frac{U_B}{I_B}=\frac{U_1+2U_2}{I_2}
\end{align*}
Podstawiając równania rozwiązań dla linii długich za $I_2$ oraz $U_2$:
\begin{align*}
Z_A=\frac{U_1}{2I_1+I_{1}\cos{\beta L}-j\frac{U_1}{Z_0}\sin{\beta L}} \\
Z_B=\frac{U_1+2U_{1}\cos{\beta L}-j2I_{1}Z_{0}\sin{\beta L}}{I_{1}\cos{\beta L}-j\frac{U_1}{Z_0}\sin{\beta L}}
\end{align*}
Są to ogólne wzory dla tego transformatora (oczywiście po przejęciu założeń co do długości linii).

1. Linia o zerowej długości (i całkowitych wielokrotności długości fali)

Na początku przyjmiemy dość abstrakcyjny przypadek, bowiem zakładamy, że linia ma zerową długość.
$L=0$, więc $\sin{\beta L}=0$ i $\cos{\beta L}=1$, zatem podstawiamy wartości i otrzymujemy:
\begin{align*}
Z_A=\frac{U_1}{3I_1} \\
Z_B=\frac{3U_1}{I_1}
\end{align*}
Po przekształceniu otrzymujemy ostateczny wniosek:
\[ Z_A=\frac{Z_B}{9} \]
Istotnie, przełożenie transformatora wynosi 1:9. Oczywiście linia zerowej długości nie ma fizycznie zbyt sensownej interpretacji. Można jednak zauważyć, że $\sin{\beta L}=0$ i $\cos{\beta L}=1$ nie tylko dla zerowej długości, ale także dla wielokrotności całej długości fali, zatem powyższy wzór będzie prawdziwy i w takich przypadkach.

2. Linia o niezerowej długości

Wróćmy jeszcze raz do ogólnych wzorów na impedancję.
Przekształcamy każde z równań tak, że po jednej stronie wyłączamy napięcie $U_1$, a po drugiej prąd $I_2$. Dostajemy następujące równania:
\begin{align*}
U_{1}(1+2\cos{\beta L}+j\frac{Z_B}{Z_0}\sin{\beta L})=I_{1}(Z_{B}\cos{\beta L}+j2Z_{0}\sin{\beta L}) \\
U_{1}(1+j\frac{Z_A}{Z_0}\sin{\beta L})=I_{1}(2Z_{A}+Z_{A}\cos{\beta L})
\end{align*}
Z jednego z równań wyliczamy np. $U_1=…$ i wstawiamy do drugiego. Otrzymujemy pojedyncze równanie i wymnażamy, żeby nie mieć ułamków. Jeden z wyrazów powinien się skrócić, a wtedy otrzymujemy:
\begin{align*}
Z_{B}\cos{\beta L}+j2Z_{0}\sin{\beta L}-2Z_{A}\sin{^2\beta L}= \\
=2Z_{A}+4Z_{A}\cos{\beta L}+j2\frac{Z_{A}Z_{B}}{Z_0}\sin{\beta L}+Z_{A}\cos{\beta L}+2Z_{A}\cos{^2\beta L}
\end{align*}
Przekształcamy tak równanie, żeby tylko po jednej stronie pojawiły się wyrazy z $Z_A$. Ponadto redukujemy jedynkę trygonometryczną (która się pojawiła) i dodajemy to, co się da. Otrzymujemy ostateczny wzór na impedancję:
\[ Z_A=\frac{Z_{B}\cos{\beta L}+j2Z_{0}\sin{\beta L}}{4+5\cos{\beta L}+j2\frac{Z_B}{Z_0}\sin{\beta L}} \]
Łatwo sprawdzić, że dla linii o zerowej długości otrzymujemy $Z_A=\frac{Z_B}{9}$.

Wiemy już, jak powyższy transformator transformuje impedancję i umiemy ją policzyć. Pytanie tylko, jak dobrać odpowiednią impedancję falową linii oraz jej długość?
Na potrzeby dalszych rozważań przyjmijmy, że impedancja z prawej strony to typowa, „radiokomunikacyjna” impedancja $Z_B=50$, a ta z lewej jest 9 razy mniejsza, więc jest równa $Z_A=5,556$.
Nie będziemy wykonywać obliczeń na drodze analizy matematycznej, a numerycznie ustalimy optymalne wartości. Załóżmy na początek, że długość linii to 5% długości fali, a więc przesunięcie fazy $\beta L=\frac{\pi}{10}$.
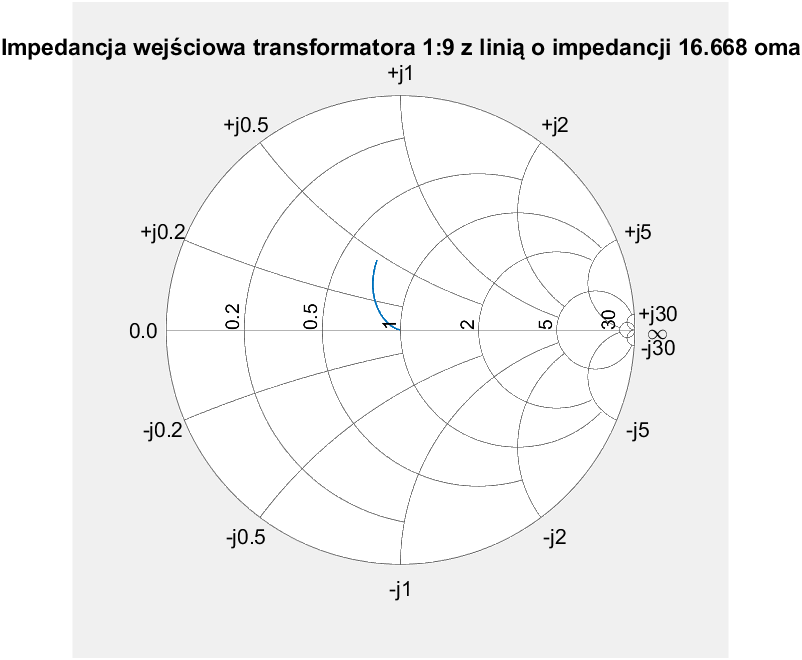
Znając docelową i rzeczywistą impedancję $Z_A$ możemy obliczyć współczynnik odbicia i SWR. Zakładam, że impedancja falowa linii ma charakter wyłącznie rzeczywisty (reaktancja jest równa zero). Dodatkowo znormalizowaną impedancję $Z_A$ przedstawiono na wykresie Smitha.

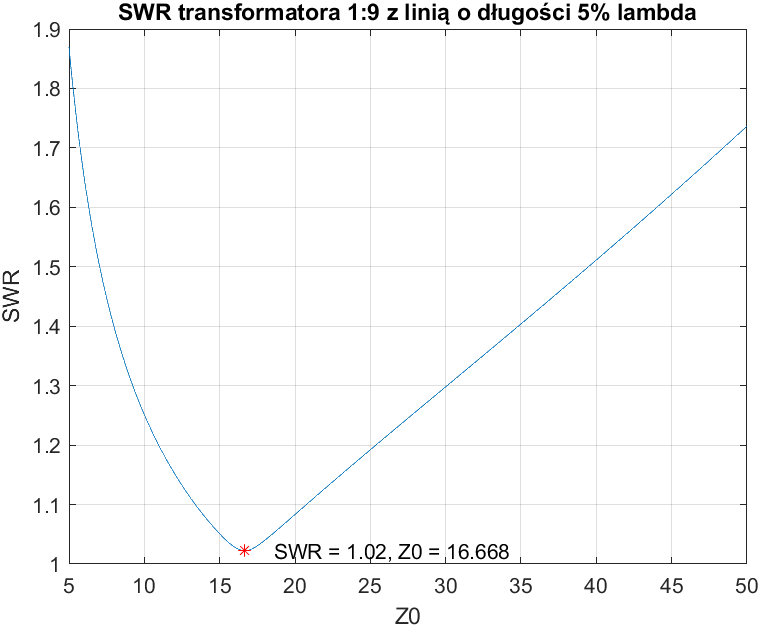
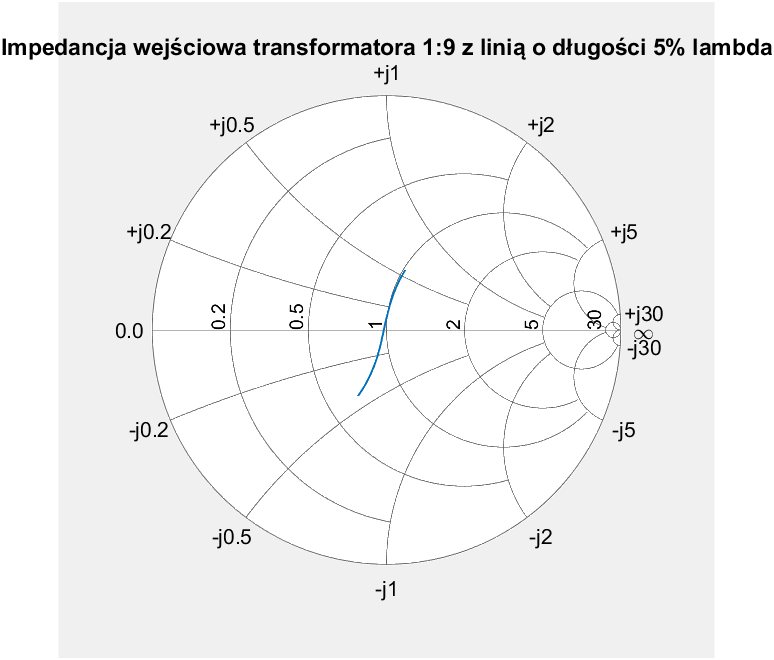
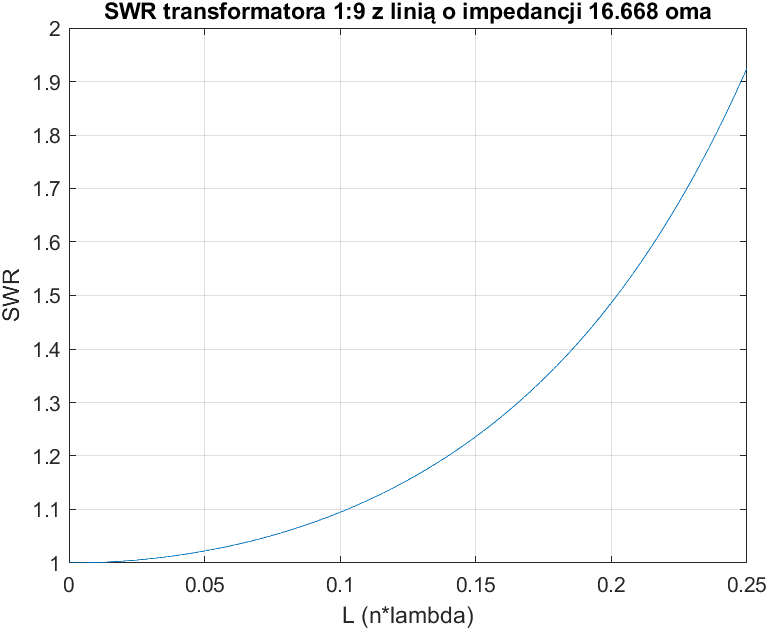
Optymalna wartość impedancji falowej jest równa $Z_0=16,668$, co w zasadzie pokrywa się ze wzorem wyprowadzonym dla pojedynczej ćwierćfalowej linii w poprzedniej części: $Z_0=\sqrt{Z_{A}Z_{B}}=16,673$, a minimalna rozbieżność wynika prawdopodobnie z błędów zaokrągleń. Można wnioskować więc, że dla krótkich linii transmisyjnych wzór ten jest prawdziwy. Warto zauważyć, że przy krótkiej linii SWR jest akceptowalny w szerokim zakresie.

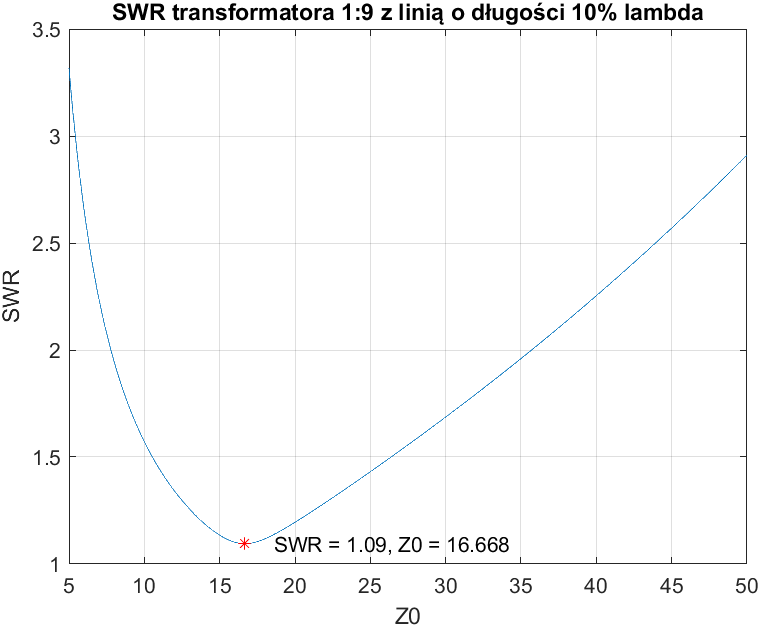
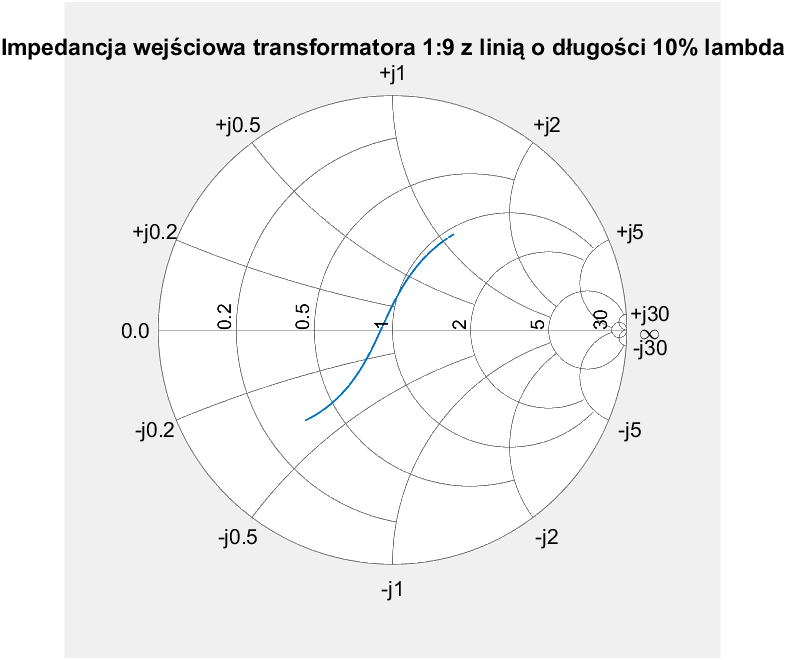
Podobnie jak poprzednio, dla linii o długości 10% długości fali optymalna impedancja falowa jest równa $Z_0=16,668$. Trzeba zauważyć jednak, że tym razem SWR wzrasta znacznie szybciej. Minimum SWRu także podniosło się.
Co ciekawe, optymalna impedancja falowa linii nie zmienia się wraz ze wzrostem jej długości.

Skoro optymalna impedancja falowa linii jest zawsze taka sama i równa, w tym przypadku, $Z_0=16,668$, to przyjmijmy ją jako stałą i sprawdźmy jak zmienia się SWR w funkcji długości linii. Ta zależność jest bardzo istotna w przypadku dopasowań szerokopasmowych, gdy elektryczna długość linii długiej zmienia się w zależności od częstotliwości.

Można także przyjrzeć się, co dzieje się dla linii o większych długościach.

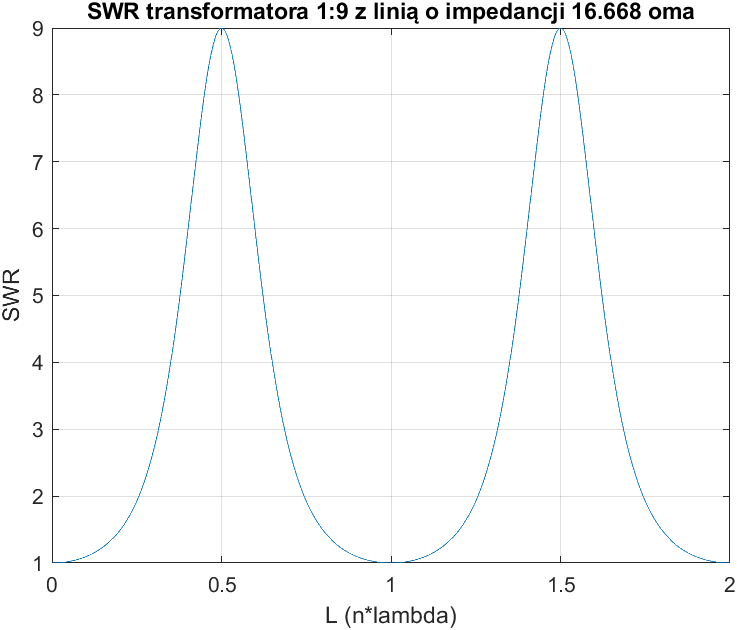
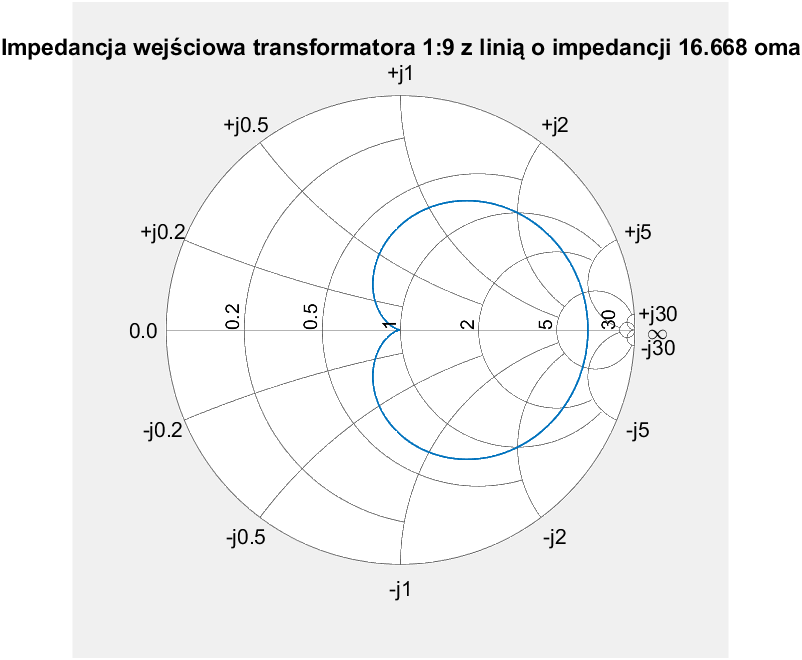
Jak widać wykresy te są symetryczne wokół punktu, gdzie linia osiąga długość połowy fali. Ponadto cały wykres powtarza się co długość fali i wynika to oczywiście z właściwości funkcji trygonometrycznych sinus i kosinus, które mają okres 360 stopni, co odpowiada jednej długości fali.
Przyglądając się tym wykresom można stwierdzić, że długość linii w transformatorze powinna być jak najmniejsza. Jednocześnie dość oczywistą rzeczą jest, że nie da się zastosować linii o (praktycznie) zerowej długości i oczekiwać, że układ taki będzie działał. W związku z tym transformatory na pasma KF nawija się krótkimi przewodami (często w okolicach 20-30 cm) na rdzeniach ferrytowych o dużej przenikalności w celu maksymalizacji sprzężenia.

Z uwagi na początkowe założenie o dozwolonych, w tym przypadku, długościach linii (która nie może być równa ćwierci długości fali lub jej nieparzystej wielokrotności), punkty odpowiadające takim długościom powinny zostać wyrzucone z dziedziny i nie brane pod uwagę w tym wykresie. Teoretycznie (z matematycznego punktu widzenia) można by się spodziewać nieciągłości funkcji w takim punkcie, niemniej w żadnych rzeczywistych układach nie mogą występować punktowe nieciągłości. Po przyjrzeniu się rysunkowi 9 można zauważyć, że w jednym z takich punktów SWR jest trochę większy od 1.9. Zaraz zajmiemy się tym szczególnym przypadkiem i sprawdzimy, czy odczytany z tego wykresu SWR jest poprawny.

Linia o długości ćwierci fali lub jej nieparzystej wielokrotności – przypadek szczególny

Przypadek szczególny, bowiem tutaj nie zostało spełnione założenie o równościach $U_4=U_2$ i $I_1=I_3$. Na początku załóżmy, że $L=\frac{\lambda}{4}$ (lub $\frac{5\lambda}{4}$, $\frac{9\lambda}{4}$ itd.), tak że $\sin{\beta L}=1$, a $\cos{\beta L}=0$.
Z prawa Ohma ustalamy najbardziej ogólny zestaw równań, opisujący ten obwód:
\begin{align*}
Z_A=\frac{U_1}{I_1+I_2+I_3} \\
Z_B=\frac{U_1+U_2+U_4}{I_2}
\end{align*}
W pierwszym równaniu za napięcie, a w drugim za prądy, wstawiamy rozwiązania równania linii długiej (podane wcześniej) oraz podstawiamy wartości funkcji trygonometrycznych:
\begin{align*}
Z_A=\frac{jI_{2}Z_{0}}{I_1+I_2+I_3} \\
Z_B=\frac{jI_{2}Z_{0}-jI_{1}Z_{0}-jI_{3}Z_{0}}{I_2}
\end{align*}

Wyłączamy $jZ_0$ z równań, odwracamy pierwsze i dodajemy oba równania stronami. Otrzymujemy:
\[ \frac{Z_B}{jZ_0}+\frac{jZ_0}{Z_A}=\frac{2I_2}{I_2} \]
Upraszczamy i przekształcamy, otrzymując:
\[ Z_{A}=-\frac{Z^2_0}{2jZ_{0}-Z_{B}} \]
Niestety nie widać tutaj nigdzie przełożenia 1:9. Zakładając, że chcemy dopasować impedancję $Z_A=5,555$ do $Z_B=50$ (1:9), impedancja falowa linii musi być równa $Z_0=15,72-j5,555$.
Co ciekawe, dla symetrycznego transformatora 1:4, w przypadku ćwierćfalowej linii, wymagana impedancja falowa jest równa $Z_0=\sqrt{Z_{A}Z_{B}}$ (co jest dość proste do udowodnienia) i jest to taki sam wzór, który wyprowadziliśmy w części 1. Jeśli tutaj chcielibyśmy go zastosować, czyli użyć linii o impedancji $Z_0=\sqrt{5,555*50}=16,667$, to wówczas przy impedancji $Z_B=50$ rzeczywista wypadkowa impedancja $Z_A=3,85+j2,56$. Czy jest to wystarczająco dobre dopasowanie? Połączenie impedancji $5,555$ z impedancją $3,85+j2,56$ skutkuje $SWR=1,92$ w tym punkcie. Warto zauważyć, że obliczony tutaj SWR pokrywa się z SWRem odczytanym z wykresu na rysunku 9.
Powstaje jeszcze pytanie: a co, gdy $\sin{\beta L}=-1$, czyli $L=\frac{3\lambda}{4}$ (lub $\frac{7\lambda}{4}$, $\frac{11\lambda}{4}$ itd.)? Sprawdzenie tego przypadku zostawiam czytelnikowi. Podpowiadam – ostateczny wynik się nie zmienia.

Na koniec uwaga: obliczenia tutaj wykonywałem sam, z czego wszystkie wzory i przekształcenia wyprowadzałem ręcznie, na kartce. Jeśli jest gdzieś błąd lub coś jest niezrozumiałe, to proszę o informację.