Spis treści:
1. Linie długie, transformacja impedancji przez linię długą
2. Transformatory z linii długiej (transmission line transformers – TLT), transformator symetryczny 1:9

Oto pierwsza część nowej serii na tym blogu, która poświęcona będzie teoretycznej analizie rozmaitych obwodów transformujących impedancję. Wydaje mi się, że jest to temat po pierwsze ciekawy, a po drugie bardzo potrzebny konstruktorom. Jeśli zastanawiasz się, dlaczego układ cewki i kondensatora pozwala dopasować bardzo wiele anten lub dlaczego rozwarty na końcu, ćwierćfalowy odcinek przewodu koncentrycznego zachowuje się od drugiej strony jakby był zwarty, to ta seria jest dla Ciebie. Nie ukrywam, że zainspirował mnie blog K6JCA.

W tym wpisie powiemy sobie trochę o liniach długich (szczególnie skupimy się na przewodach koncentrycznych), wyprowadzimy wzory opisujące napięcia i prądy w takiej linii oraz znajdziemy wzór opisujący transformację impedancji przez linię długą o określonej długości i impedancji falowej. Na wstępie zaznaczam, że nie będą tutaj omawiane podstawy elektrotechniki i matematyki.

Linia długa to przewód zbudowany z dwóch przewodników, służący do przenoszenia sygnałów. W krótkofalarstwie najczęstszym spotykanym typem linii długich jest przewód koncentryczny lub symetryczny (tzw. drabinka). Linia długa nie bez powodu nazywana jest długą… Jeśli jej fizyczna długość (a w zasadzie to elektryczna – istnieje współczynnik skrócenia, więc fala w przewodniku będzie krótsza niż w próżni) stanowi znaczącą część długości fali przesyłanego sygnału, to linia taka zaczyna mieć istotny wpływ na prądy i napięcia w obwodzie – czyli nie można zaniedbać jej wpływu. Granica, przy której linia staje się długą, jest dość umowna i zależna od danego przypadku, ale bardzo bezpiecznie jest przyjąć, iż linia o elektrycznej długości 5% długości fali jest już linią długą.

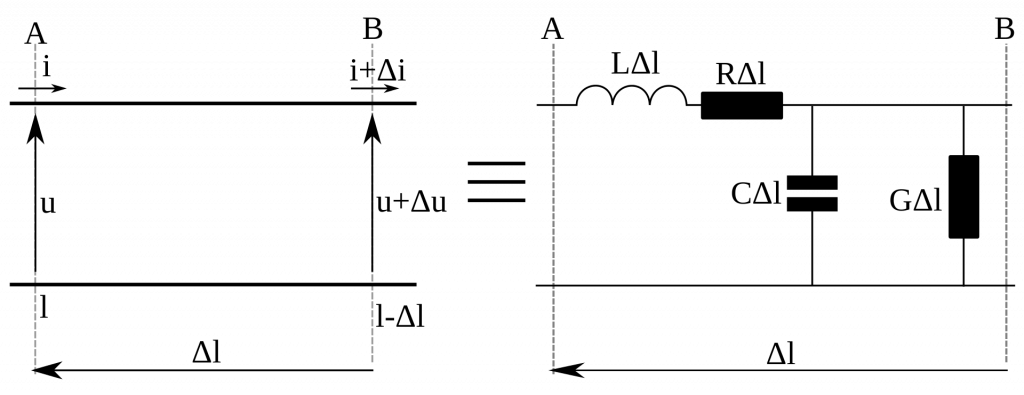
Linia długa składa się z dwóch przewodników oddzielonych izolatorem. Jak wiadomo, każdy przewodnik posiada rezystancję, oznaczoną na rysunku przez R. Tak samo każdy przewodnik z prądem wytwarza pole magnetyczne, więc ma własną indukcyjność, oznaczoną przez L. Pomiędzy dwoma przewodnikami tworzy się pewna indukcyjność, oznaczona przez C. Dodatkowo izolator między przewodami nie jest doskonały i jego rezystancja jest skończona (choć bardzo duża), tutaj oznaczono konduktancję izolatora G.

W każdej linii transmisyjnej przypadają jakieś (określone) wartości R, G, L i C na jednostkę długości. Wielkości te zmieniają się liniowo wraz ze zmianą długości linii.
Rezystancja R i konduktancja G są odpowiedzialne przede wszystkim za straty w linii długiej, natomiast indukcyjność L i pojemność C wyznaczają przede wszystkim impedancję charakterystyczną (falową) linii. Impedancja falowa linii długiej jest równa:

\[ Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}} \]

Jest to liczba zespolona, a wynikowa impedancja jest zależna od wszystkich parametrów linii. Można zauważyć, że w przypadku rzeczywistej (stratnej) linii impedancja ta jest również zależna od pulsacji, a więc i częstotliwości. Dla uproszczenia obliczeń przyjmiemy, że linia jest bezstratna, tj. R=0 i G=0. Wówczas:

\[ Z_0=\sqrt{\frac{L}{C}} \]

Impedancja falowa jest taka sama w każdym punkcie linii długiej, tzn. w każdym punkcie linii długiej stosunek napięcia do prądu jest stały i równy impedancji falowej (bardzo ważna własność!):

\[ Z_0=\frac{U(x)}{I(x)} \]

Fala elektromagnetyczna/elektryczna w danym ośrodku rozchodzi się ze skończoną prędkością. W przypadku próżni fala EM rozchodzi się z prędkością światła, więc pokonanie jakiegoś dystansu zajmuje jej określoną ilość czasu. Nie inaczej jest w przypadku linii długich – w przewodnikach fala taka również rozchodzi się z określoną prędkością (mniejszą niż prędkość światła), więc pokonanie długości linii także zajmuje jej określoną ilość czasu, zatem wprowadzone jest opóźnienie, które matematycznie opisujemy jako przesunięcie fazy.
Istotnym parametrem linii długiej jest stała propagacji, określająca tłumienie i przesunięcie fazy sygnału przesyłanego tą linią:

\[ \gamma=\sqrt{(R+j\omega L)(G+j\omega C)}=\alpha +j\beta \]
Gdzie $\alpha$ to stała tłumienia (przyjmujemy linię bezstratną, więc stała tłumienia jest równa 0), a $\beta$ to stała fazowa, która określa omówione wyżej opóźnienie (przesunięcie fazy) sygnału przewodzonego przez linię. Stała fazowa jest liczbowo tym samym, co liczba falowa $k$ (znana z fizyki) i oznaczenia te są zamiennie wykorzystywane.

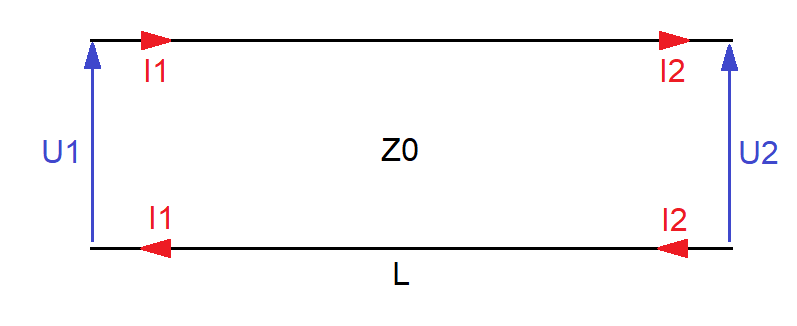
Do opisu linii długich używa się tzw. równań telegrafistów, które wyprowadza się z przedstawionego wyżej (rys. 1) elektrycznego modelu linii długiej. Jest to zestaw dwóch równań różniczkowych opisujących napięcie oraz prąd w dowolnym punkcie linii. Dla linii bezstratnej, w stanie ustalonym sinusoidalnym, równania te wyglądają następująco:

\begin{align*}
\frac{d^2U}{dx^2}+\beta^2U=0 \\
\frac{d^2I}{dx^2}+\beta^2I=0
\end{align*}

Ich rozwiązania wyglądają następująco:

\begin{align*}
U(x)=U_{+}e^{-j\beta x}+U_{-}e^{j\beta x} \\
I(x)=I_{+}e^{-j\beta x}-I_{-}e^{j\beta x}
\end{align*}
W linii długiej fala może poruszać się w dwie strony, z tego powodu we wzorze pojawiają się napięcia oznaczone przez $U_+$ i $U_-$ oraz odpowiadające im prądy $I_+$ i $I_-$, gdzie indeks $+$ oznacza falę postępującą (poruszającą się w prawo), a indeks $-$ falę odbitą (poruszającą się w lewo). Jak nietrudno zauważyć, w podanych wzorach wypadkowe napięcie jest sumą napięć składowych, a wypadkowy prąd jest różnicą prądu fali postępującej i odbitej. Takie rozumowanie jest poprawne dla założeń jak na rysunku 2, gdzie prądy w górnej gałęzi płyną w prawą stronę, a napięcia zwrócone są „do góry”.
Przyjmijmy, że operujemy na wartościach w punkcie $x$, więc porzućmy $(x)$. Używając wzorów Eulera, można równania te rozłożyć na postać trygonometryczną.
\begin{align*}
U=U_{+}(\cos{\beta x}-j\sin{\beta x})+U_{-}(\cos{\beta x}+j\sin{\beta x}) \\
I=I_{+}(\cos{\beta x}-j\sin{\beta x})-I_{-}(\cos{\beta x}+j\sin{\beta x})
\end{align*}
Będą to kluczowe wzory przy dalszych rozważaniach nt. linii długich.
Równania te zawierają funkcje trygonometryczne, które opisują przesunięcia opóźnienia napięcia i prądu (przesunięcie faz), bo sygnał potrzebuje skończonego czasu na przebycie całej długości linii. We wzorach przez $x$ oznaczono odległość od jednego końca linii, a przez $\beta$, omówioną wcześniej, stałą fazową, która równa jest $\beta=\frac{2\pi f}{Kc}=\frac{2\pi K}{\lambda}$, gdzie $f$ jest częstotliwością, $c$ prędkością światła, $K$ współczynnikiem skrócenia fali, a $\lambda$ długością fali w próżni. Całościowo $\beta x$ jest kątem przesunięcia fali po przejściu przez odcinek linii długiej o długości $x$, np. dla $x=\frac{\lambda}{4}$ (przy uwzględnieniu współczynnika skrócenia) kąt ten jest równy $\frac{\pi}{2}$.

Możemy teraz wyznaczyć napięcia i prądy na końcach linii długiej. Na początek wyznaczymy $U_2$ i $I_2$ (prawa strona linii), które będą zależne od $U_1$ i $I_1$ (lewa strona linii) – będzie to punkt odniesienia. Zakładamy, że wartości na prawo od $x=0$ są dodatnie, a na lewo – ujemne. Innymi słowy wartości na osi $x$ „rosną w prawo”. Punkt odniesienia traktujemy jako punkt $x=0$ i podstawiamy do wzoru. Otrzymujemy:
\begin{align*}
U_1=U_{+}(\cos{0}-j\sin{0})+U_{-}(\cos{0}+j\sin{0}) \\
I_1=I_{+}(\cos{0}-j\sin{0})-I_{-}(\cos{0}+j\sin{0})
\end{align*}
zatem:
\begin{align*}
U_1=U_{+}+U_{-} \\
I_1=I_{+}-I_{-}
\end{align*}
Wiedząc, że $I_x=\frac{U_x}{Z_0}$ (żeby pozbyć się prądów) przekształcamy równania i otrzymujemy:
\begin{align*}
U_+=\frac{U_1+I_{1}Z_0}{2} \\
U_-=\frac{U_1-I_{1}Z_0}{2}
\end{align*}
Fala pokonuje drogę od punktu $x=0$ do $x=L$, więc przemieszczenie jest równe $L$ – istnieje niezerowe opóźnienie (przesunięcie fazy) fali przy przemieszczaniu się jej z lewego do prawego końca linii. Prądy i napięcia są zgodne na całej długości linii (zgodnie z rysunkiem), więc ponownie korzystamy z tego samego wzoru i podstawiamy wartości. Otrzymujemy:
\begin{align*}
U_2=U_{+}(\cos{\beta L}-j\sin{\beta L})+U_{-}(\cos{\beta L}+j\sin{\beta L}) \\
I_2=I_{+}(\cos{\beta L}-j\sin{\beta L})-I_{-}(\cos{\beta L}+j\sin{\beta L})
\end{align*}
Wstawiamy wyznaczone wcześniej $U_+$ i $U_-$ (napięcia w punkcie odniesienia) i otrzymujemy ostatecznie:
\begin{align*}
U_2=U_{1}\cos{\beta L}-jI_{1}Z_{0}\sin{\beta L} \\
I_2=I_{1}\cos{\beta L}-j\frac{U_{1}}{Z_{0}}\sin{\beta L}
\end{align*}

Analogiczne rozumowanie przeprowadzimy, żeby wyprowadzić wzory na $U_1$ i $I_1$ w zależności od $U_2$ i $I_2$ (czyli w drugą stronę). Tym razem punktem odniesienia jest prawa strona, więc w tym miejscu przyjmujemy $x=0$:
\begin{align*}
U_2=U_{+}+U_{-} \\
I_2=I_{+}-I_{-}
\end{align*}
Trzeba zauważyć, że nadal fala postępująca przemieszcza się w prawo, a odbita w lewo.
Podobnie przekształcamy i otrzymujemy:
\begin{align*}
U_+=\frac{U_2+I_{2}Z_0}{2} \\
U_-=\frac{U_2-I_{2}Z_0}{2}
\end{align*}
Tutaj jednak następuje pewna zmiana. Przyjęliśmy prawą stronę linii jako punkt odniesienia $x=0$, a także że wartości na osi rosną w prawo, zatem lewa strona linii leży w punkcie $x=-L$, tym samym przemieszczenie fali jest równe $-L$.
\begin{align*}
U_1=U_{+}(\cos{\beta L}+j\sin{\beta L})+U_{-}(\cos{\beta L}-j\sin{\beta L}) \\
I_1=I_{+}(\cos{\beta L}+j\sin{\beta L})-I_{-}(\cos{\beta L}-j\sin{\beta L})
\end{align*}
Funkcja cosinus jest parzysta, zatem $-$ w jej argumencie znika. Sinus jest nieparzysty, więc $-$ można przenieść z argumentu do wartości funkcji. W porównaniu z poprzednimi wzorami zmieniły się tylko znaki przed funkcjami $sin$.
Ponownie podstawiamy obliczone $U_+$ i $U_-$ i otrzymujemy ostatecznie:
\begin{align*}
U_1=U_{2}\cos{\beta L}+jI_{2}Z_{0}\sin{\beta L} \\
I_1=I_{2}\cos{\beta L}+j\frac{U_{2}}{Z_{0}}\sin{\beta L}
\end{align*}

Zdecydowanie najgorsze już za nami. Celem tej serii jest omówienie mechanizmów transformacji impedancji, a linie długie „potrafią” impedancje przekształcać. Na rysunku poniżej zaprezentowano linię długą obciążoną impedancją. Powstaje pytanie, jaka będzie impedancja „widziana” z drugiego końca linii?

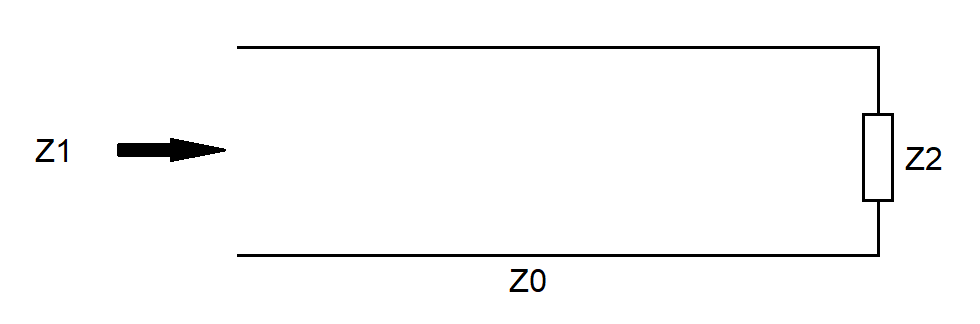
Przyjmujemy jak poprzednio, tzn. po prawej stronie linii napięcie $U_2$ i prąd $I_2$, a po lewej $U_1$ i $I_1$, napięcia zwrócone do góry, a prądy płyną w prawo w górnej gałęzi. Korzystamy z wyprowadzonych wzorów na $U_1$ i $U_2$ i prawa Ohma, które mówi, że $Z_1=\frac{U_1}{I_1}$, zatem:
\[ Z_1=\frac{U_{2}\cos{\beta L}+jI_{2}Z_{0}\sin{\beta L}}{I_{2}\cos{\beta L}+j\frac{U_{2}}{Z_{0}}\sin{\beta L}} \]
Z prawa Ohma wiadomo także, że $Z_2=\frac{U_2}{I_2}$, więc ułamek po prawej stronie równania można skrócić (podzielić licznik i mianownik) przez $I_2$, wówczas:
\[ Z_1=\frac{Z_{2}\cos{\beta L}+jZ_{0}\sin{\beta L}}{\cos{\beta L}+j\frac{Z_{2}}{Z_{0}}\sin{\beta L}} \]
Jest to ogólny wzór pozwalający obliczyć impedancję na drugim końcu linii długiej.

Przy tej okazji przytoczę ważne twierdzenie (które jest w pewnym sensie definicją impedancji falowej), które mówi, że jeśli linię długą o impedancji $Z_0$ obciążymy impedancją $Z_2$, która jest równa impedancji falowej linii, to impedancja $Z_1$ „widziana” z drugiej strony linii będzie równa tym impedancjom, tzn. jeśli $Z_2=Z_0$, to $Z_1=Z_2=Z_0$. Udowodnienie tego jest proste. Korzystamy z wyprowadzonego przed chwilą wzoru i podstawiamy $Z_2=Z_0$:
\[ Z_1=\frac{Z_{0}\cos{\beta L}+jZ_{0}\sin{\beta L}}{\cos{\beta L}+j\sin{\beta L}} \]
Wyłączamy $Z_0$ przed nawias, a reszta się upraszcza. Ostatecznie:
\[ Z_1=Z_0 \]
Jest to przypadek zwany dopasowaniem falowym. Widać, że przy takim dopasowaniu linia długa jest „przezroczysta” i impedancja nie jest zależna od długości linii. Jeśli łączymy dobrze dostrojoną antenę z nadajnikiem (czyli ich impedancje są równe), to długość przewodu nie będzie miała żadnego wpływu na SWR (o ile sam przewód nie wprowadza znaczących strat ani nie jest częścią anteny).

Kolejną ciekawą właściwością jest transformacja impedancji przez ćwierćfalową linię długą, np. ćwierćfalowa linia zwarta na jednym końcu jest widoczna z drugiego końca jako rozwarta, a rozwarta – jako zwarta. Taka właściwość jest dość często przytaczana w różnych rozważaniach, a także wykorzystywana np. w filtrach czy przełącznikach, więc teraz udowodnimy, że tak rzeczywiście jest.
Zaczniemy od wyznaczenia wartości przesunięć fazy. Linia o długości $\frac{\lambda}{4}$ (ćwierćfalowa) przesuwa falę o ćwierć jej długości, co kątowo daje 90 stopni, czyli $\frac{\pi}{2}$ radianów. Tym samym $\beta x=\frac{\pi}{2}$, a więc $\sin{\beta x}=1$ i $\cos{\beta x}=0$. Podstawiamy do wzoru i otrzymujemy:
\[ Z_1=\frac{jZ_{0}}{j\frac{Z_{2}}{Z_{0}}} \]
Po dodatkowym uproszczeniu:
\[ Z_1=\frac{Z^{2}_{0}}{Z_2} \]
Oczywiście zwarcie linii na końcu powoduje, że $Z_2=0$ i wartość całego ułamka dąży do nieskończoności, więc impedancja na wejściu również dąży do nieskończoności (co interpretujemy jako rozwarcie). Odwrotnie dzieje się dla rozwarcia: $Z_2=\infty$, wartość ułamka i impedancji wejściowej dąży do 0. Ale z tego równania można wyciągnąć jeszcze więcej. Po prostym przekształceniu otrzymujemy wzór, który dość często przewija się w temacie transformatorów, fazowania anten itp.:
\[ \sqrt{Z_{1}Z_{2}}=Z_{0} \]
Wynika z niego, że do dopasowania dwóch różnych impedancji $Z_1$ i $Z_2$ wystarczy użyć ćwierćfalowej linii długiej o określonej impedancji $Z_0$. Warto go zapamiętać. Ponadto można skorzystać z własności funkcji trygonometrycznych i zauważyć, że taki sam efekt da zastosowanie linii o długości równej nieparzystej wielokrotności ćwierci długości fali.

Jako dodatek rozważymy jeszcze przypadek takiej samej linii długiej, ale z inaczej oznaczonymi prądami. Ta analiza ma na celu zapobieganie błędom podczas używania wzorów bez zrozumienia ich w całości. Oznaczmy napięcia i prądy na linii długiej jak pokazano na rysunku 4:

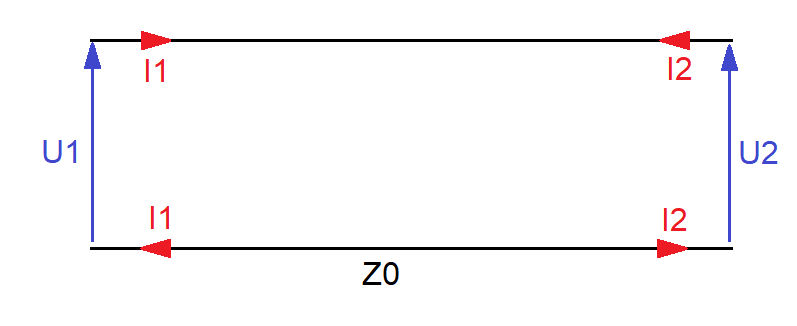
Tutaj prądy mają przeciwne zwroty. Bez uwzględniania przesunięć fazy (przyjmujemy cały czas $x=0$) prąd $I_1=I_{+}-I_{-}$ (tak jak poprzednio), natomiast $I_2=-(I_{+}-I_{-})$, czyli prąd $I_2$ jest po prostu przeciwny. Przeprowadzamy rozumowanie jak poprzednio, tzn. przyjmujemy lewą stronę za punkt odniesienia $x=0$, wówczas po przekształceniach:
\begin{align*}
U_+=\frac{U_1+I_{1}Z_0}{2} \\
U_-=\frac{U_1-I_{1}Z_0}{2}
\end{align*}
Są to te same wzory, co poprzednio, bo prąd po lewej jest zwrócony w tę samą stronę.
Przypominamy rozwiązania równań telegrafistów, ale teraz prąd $I_2$ będzie przeciwny (jak ustaliliśmy wcześniej). Przemieszczenie po linii jest równe $L$, zatem:
\begin{align*}
U_2=U_{+}(\cos{\beta L}-j\sin{\beta L})+U_{-}(\cos{\beta L}+j\sin{\beta L}) \\
I_2=-(I_{+}(\cos{\beta L}-j\sin{\beta L})-I_{-}(\cos{\beta L}+j\sin{\beta L}))
\end{align*}
Uwaga! Nie możemy po prostu zamienić miejscami prądu fali postępującej i odbitej, bo są one powiązane z przesunięciami fazy.
Ostatecznie otrzymujemy:
\begin{align*}
U_2=U_{1}\cos{\beta L}-jI_{1}Z_{0}\sin{\beta L} \\
I_2=-I_{1}\cos{\beta L}+j\frac{U_{1}}{Z_{0}}\sin{\beta L}
\end{align*}

Analogiczne rozumowanie przeprowadzimy dla drugiej strony linii. Przyjmujemy za punkt odniesienia prawą stronę. Trzeba zauważyć, że tutaj prąd skierowany jest w przeciwną stronę, więc $I_2=I_{-}-I_{+}$.
\begin{align*}
U_+=\frac{U_1-I_{1}Z_0}{2} \\
U_-=\frac{U_1+I_{1}Z_0}{2}
\end{align*}
Jak widać, tym razem znaki przy prądach zostały odwrócone.
Korzystamy z rozwiązań równań telegrafistów. Prąd $I_1$ pozostaje skierowany w prawo, więc nie będziemy zmieniać znaku. Oczywiście tym razem przemieszczenie jest równe $-L$:
\begin{align*}
U_1=U_{+}(\cos{\beta L}+j\sin{\beta L})+U_{-}(\cos{\beta L}-j\sin{\beta L}) \\
I_1=-(I_{+}(\cos{\beta L}+j\sin{\beta L})-I_{-}(\cos{\beta L}-j\sin{\beta L}))
\end{align*}
Ostatecznie:
\begin{align*}
U_1=U_{2}\cos{\beta L}-jI_{2}Z_{0}\sin{\beta L} \\
I_1=-I_{2}\cos{\beta L}+j\frac{U_{2}}{Z_{0}}\sin{\beta L}
\end{align*}
Co ciekawe, równania na prądy i napięcia po obydwu stronach linii mają taką samą formę. Stało się tak dlatego, że nie występuje tutaj „asymetria”, tzn. z obydwu stron prądy wpływają do linii. W przypadku, który rozważaliśmy jako pierwszy, taka „asymetria” występuje (z jednej strony prąd wpływa, z drugiej wypływa), więc równania mają różne formy.

W następnej części zajmujemy się praktycznym wykorzystaniem linii długich w budowie transformatorów TLT oraz analizujemy symetryczny transformator 1:9.